L’utilité espérée (Bernoulli, 1738/1971) n’est pas une conception directement liée à la motivation mais à la prise de décision. Cependant, cette conception, bien que d’essence mathématique, introduit une évaluation sur ce qui « pousse » l’être humain à rechercher les gains et à éviter les pertes dans les situations où il doit faire des paris. En effet, Bernoulli avait observé que l’homme n’agit pas de façon totalement rationnelle, c’est-à-dire de manière conforme à ce que prédisent les lois mathématiques en termes de probabilités, lorsqu’il est confronté aux jeux de hasard. Si l’individu était parfaitement rationnel, au sens mathématique du terme, ses choix devraient toujours être conformes à l’espérance mathématique qui peut être défini comme suit :
« Les valeurs espérées se calculent en multipliant chaque gain possible par le nombre des possibilités de l’atteindre, et en divisant la somme des produits obtenus par le nombre total des cas possibles, étant bien observé qu’il importe, dans cette théorie, que les cas considérés aient tous la même probabilité » (Bernoulli, 1738/1971, p 5).
Cependant, l’espérance mathématique est clairement mise en défaut dans les jeux de hasard, l’individu ayant tendance à se montrer moins gourmand que ce que prédit l’espérance mathématique (ce que Bernoulli montre au travers du paradoxe de Saint Pétersbourg). C’est pour tenir compte du comportement humain dans les situations de risque qu’il propose le concept d’utilité espérée.
« De quelque façon, une personne très pauvre est mise en possession d’un billet d’une loterie qui peut, avec une égale probabilité lui faire gagner soit rien, soit vingt mille ducats. Cette personne estimera-t-elle sa chance de gain à dix mille ducats ? N’aurait-elle pas tort de céder le billet de loterie pour neuf mille ducats ? Il me semble personnellement qu’il faudrait répondre par la négative. D’un autre côté, j’incline à penser qu’un homme riche serait mal inspiré s’il refusait d’acheter le billet pour neuf mille ducats. Si je ne me trompe, il paraît évident que tout le monde ne peut pas appliquer la règle pour évaluer le jeu. La règle du § 1(l’espérance mathématique) doit donc être écartée. Mais, toute personne qui considérera le problème avec perspicacité et intérêt, se convaincra que le concept de VALEUR dont nous nous sommes servis dans la règle doit être défini d’une manière qui rende la méthode universellement acceptable sans réserve. Pour ce faire, la détermination de la VALEUR d’un article ne sera pas fondée sur son prix, mais sur l’UTILITE qu’il procure. Le prix d’un article ne dépend que de l’objet lui-même ; il est le même pour toute personne ; en revanche l’utilité dépend des conditions particulières où se trouve la personne qui a la charge de l’évaluation. Ainsi il n’est pas douteux que le gain de mille ducats est plus important pour un homme pauvre que pour un riche, bien que le montant soit le même pour l’un et pour l’autre. » (Bernoulli, 1738/1971, p. 6).
L’utilité espérée, d’un point de vue psychologique, est donc une proposition qui renvoie à la valeur « psychologique » que chaque individu accorde à un bien, qui par ailleurs peut avoir une valeur monétaire totalement différente. L’équation que propose Bernoulli, reposant sur cette conception de la valeur en tant qu’utilité espérée, permet à l’individu de prendre ses décisions en fonction du résultat de cette équation. Il est possible de résumer la proposition de Bernouilli en disant que l’utilité de l’éventualité incertaine est la somme de toutes les utilités de tous les résultats pondérés par leur probabilité. Même si les équations de Bernoulli ont depuis été remises en cause (Camerer, 1989), la conception de l’utilité espérée imprègne aujourd’hui encore, non seulement le monde économique, mais aussi celui de la psychologie. Pour les théories motivationnelles de l’expectation et de la valeur, la motivation de l’individu dépend de la valeur que représente pour lui un résultat et de la probabilité que ce résultat se produise. La théorie de l’utilité espérée permet de préciser dans quelle condition ces deux termes devraient inciter l’individu à prendre ou non la décision d’agir. Il apparaît également que les propriétés de l’homme économique telles qu’elles ont été décrites par Edwards (1954) se retrouvent dans de nombreux modèles psychologiques de la motivation.
Pour Edwards (1954), l’homme économique (1) dispose de toute l’information disponible (il connaît toutes les alternatives de ses choix), (2) est infiniment sensible, (3) est rationnel. De plus, l’homme économique prend ses décisions en vertu de la maximisation de l’utilité espérée. Ce principe de maximisation repose sur l’hédonisme et c’est à ce niveau que les théories économiques et motivationnelles se rejoignent sans doute le plus. En effet, comme l’explique Weiner (1992), les théories de la motivation partent du principe que l’homme recherche le plaisir et évite la douleur (principe de l’hédonisme). De même, pour l’homme économique, tout objet ou action peut être envisagé sous ses aspects de plaisir et de douleur. Ces deux propriétés ou utilités de l’objet peuvent prendre une valeur positive (plaisir) et une valeur négative (douleur). Le but de toute action humaine, d’un point de vue économique serait donc de rechercher le maximum d’utilité. Autrement dit, lorsque les individus ont plusieurs choix possibles, ils choisissent l’alternative qui présente le meilleur rapport entre l’utilité positive et négative. Le modèle d’Atkinson (1964) comme tous les modèles de l’expectation-valeur en général s’inscrivent dans cette perspective de maximisation de l’utilité.
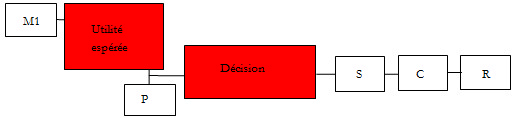
Représentation intégrée de l’utilité espérée (d’après Bernoulli, 1738)