Dans une des expériences de Hoppe (1930, cité par Nuttin, 1975), le sujet doit suspendre des anneaux à des crochets fixés sur une bande roulante qui passe devant lui à une vitesse réglable. Cette tâche comporte plusieurs phases. Dans un premier temps, l’individu se familiarise avec la tâche au travers d’une dizaine d’essais. Après cette phase d’habituation, l’expérimentateur demande explicitement au sujet combien d’anneaux il va essayer de mettre dans les crochets au prochain essai. La perception d’une réussite ou d’un d’échec dépend de l’objectif que l’individu s’efforce d’atteindre. L’échec survient si l’individu n’arrive pas à atteindre le niveau d’accomplissement qu’il s’est fixé.
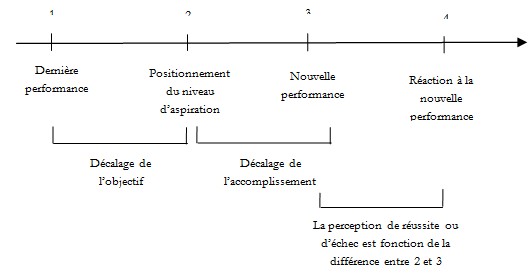
Il est à noter que dans les paradigmes de ce type tous les choix concevables, toutes les probabilités et toutes les valeurs sont connus à l’avance. Nous sommes donc dans un cas particulier où l’ensemble de l’information est disponible. Dans ces conditions, c’est le choix qui est associé à la valeur la plus importante qui est théoriquement sélectionnée par l’individu (raisonnement en termes de coût/bénéfice). C’est dans un tel contexte que Lewin, Dembo, Festinger & Sears (1944) proposent une formalisation séquentielle du niveau d’aspiration (voir figure).
L’objectif que se fixe l’individu dépend de son score antérieur. Généralement, le niveau d’aspiration décroît lorsque l’individu échoue et augmente lorsqu’il réussit. Bien que des réactions atypiques puissent également être observées quand l’individu augmente son niveau d’aspiration après un échec ou le diminue après une réussite. En effet, les individus qui ont le meilleur taux de réussite sont ceux qui se fixent des buts réalistes. À l’opposé, ceux qui ont un faible taux de réussite ont tendance à se fixer des objectifs, soit extrêmement élevés et irréalistes, soit très faibles d’où la présence d’objectifs atypiques. Les individus avec des aptitudes élevées, ou ceux avec une forte ambition, ont tendance à avoir un niveau d’aspiration très élevé. L’échec et la réussite dépendent des caractéristiques individuelles des sujets. Si l’individu a un niveau d’aspiration très élevé, le simple fait d’atteindre l’objectif qu’il s’est fixé peut être considéré comme insuffisant.
Figure. Séquence des événements dans le cadre des expériences sur le niveau d’aspiration (Lewin & al., 1944).
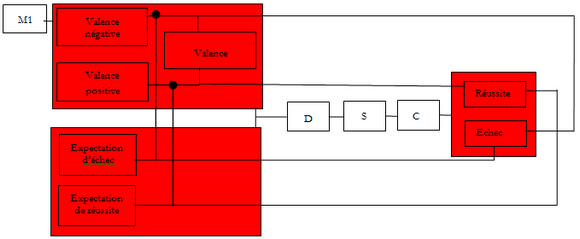
La théorie de la valence résultante (Lewin & al., 1944) permet, dans le cadre de l’étude du niveau d’aspiration, de prédire les choix des individus en fonction de différents paramètres. L’un de ces paramètres est la valence et cette dernière varie en fonction du niveau de difficulté. Chaque niveau de difficulté a une valence positive en cas de succès et une valence négative en cas d’échec. La valence positive (Vas) du succès augmente en fonction de l’augmentation du niveau de difficulté, et ce, jusqu’à une limite supérieure au-delà de laquelle l’individu estime que la réussite est totalement hors de sa portée. À l’inverse la valence négative de l’échec (Vae) est inversement proportionnelle à la difficulté de l’activité. Autrement dit, plus l’activité est facile plus l’échec est cuisant. La somme des différences entre les valences permet de prédire que la valence totale augmente en même temps que le niveau de difficulté. Il en résulte que l’individu devrait toujours faire son choix à la limite de ce qu’il peut faire or, comme nous avons pu le voir plus haut, ils ont plutôt tendance à choisir une difficulté moyenne.
La raison de cette préférence, pour un choix en termes de difficulté moyenne, est liée à la présence d’un deuxième facteur, l’expectation de succès. Ce dernier se définit comme la probabilité subjective ou « potency » de succès (Ps) ou d’échec (Pe). Ainsi, la difficulté de l’activité augmente sa valence mais parallèlement diminue la probabilité de la réussite. La valence pondérée du succès se définit donc comme la valence positive (Vas) multipliée par la probabilité de succès (Ps). La valence pondérée de l’échec est la valence négative de l’échec (Vae) multipliée par la probabilité de l’échec (Pe). La somme des deux valences pondérées permet d’obtenir la valence résultante (Vs) :
Vs = (Vas x Ps)+( Vae x Pe).
Représentation intégrée de la théorie de la valence résultante
(d’après Lewin & al., 1944)